Simulating Network Diffusion with R
Cheng-Jun Wang
06/03/2014
Introduction
In this talk, I present how to simulate the most simple network diffusion with R. The algorithm is quite simple:
- Generate a network g: g(V, E).
- Randomly select one or n nodes as seeds.
- Each infected node influences its neighbors with probability p (transmission rate, β).
SI model
Actually, this is the most basic epidemic model (SI model) with only two states: Susceptible (S) and Infected (I)! However, we will extend it to networks. Given the transmission rate \( \beta \), SI model can be described as:
\( \frac{dS}{dt}=-\beta SI \)
\( \frac{dI}{dt}=\beta SI \)
Note that I + S = 1, the equation \( \frac{dI}{dt}=\beta SI \) can be simplified as: \( \frac{dI}{dt}=\beta I(1-I) \)
Solve this equation, we can get a logistic growth function featured by its s-shaped curve.
Bring network back


R and igraph
R

igraph

To-do list
- Set transmission rate
- Update graphs
- Generate networks
- Initiate the diffusers
- Start the contagion!
- Save as the animation
Set transmission rate
Method 1
transmission_rate = 0.4
coins = c(rep(1, transmission_rate*1000), rep(0,(1-transmission_rate)*1000))
n = length(coins)
toss = function(freq) { # toss the coins
tossing = NULL
for (i in 1:freq ) tossing[i] = sample(coins, 1, replace=TRUE, prob=rep(1/n, times=n))
tossing = sum(tossing)
return (tossing)
}
Set transmission rate (Updated)
Method 2
transmission_rate = 0.4
coins = c(1, 0)
probabilities = c(transmission_rate, 1-transmission_rate )
# sample(coins, 1, rep=TRUE, prob=probabilities) # Generate a sequence
# toss the coins
toss = function(freq) {
tossing = NULL
for (i in 1:freq ) tossing[i] = sample(coins, 1, rep=TRUE, prob=probabilities)
tossing = sum(tossing)
return (tossing)
}
Update graphs
update_diffusers = function(diffusers){
nearest_neighbors = data.frame(table(unlist(neighborhood(g, 1, diffusers))))
nearest_neighbors = subset(nearest_neighbors, !(nearest_neighbors[,1]%in%diffusers))
keep = unlist(lapply(nearest_neighbors[,2], toss))
new_infected = as.numeric(as.character(nearest_neighbors[,1][keep >= 1]))
diffusers = unique(c(diffusers, new_infected))
return(diffusers)
}
Generate networks (Part 1)
Set the node_number of social graph
node_number = 100
library(igraph)
node_number
[1] 100
Generate regular networks
g = graph.tree(node_number, children = 2)
g = graph.star(node_number)
g = graph.full(node_number)
g = graph.ring(node_number)
g = connect.neighborhood(graph.ring(node_number), 2)
Generate networks (Part 2)
g = erdos.renyi.game(node_number, 0.1)
g = rewire.edges( graph.ring(node_number), prob = 0.8 )
g = watts.strogatz.game(1,node_number,3,0.2)
g = barabasi.game(node_number)
graph_name = "Scale-free network"
plot(g)
Initiate the diffusers (Part 1)
seed_num = 1
set.seed(20140301); diffusers = sample(V(g),seed_num)
infected =list()
infected[[1]]= diffusers
# set the color
E(g)$color = "grey"
V(g)$color = "white"
Initiate the diffusers (Part 2)
set.seed(2014); layout.old = layout.fruchterman.reingold(g, niter = 1000)
V(g)$color[V(g)%in%diffusers] = "red"
plot(g, layout =layout.old)
Start the contagion!
total_time = 1
while(length(infected[[total_time]]) < node_number){
infected[[total_time+1]] = sort(update_diffusers(infected[[total_time]]))
cat(length(infected[[total_time+1]]), "-->")
total_time = total_time + 1
}
2 -->14 -->22 -->29 -->36 -->50 -->59 -->67 -->75 -->80 -->85 -->87 -->88 -->92 -->94 -->97 -->98 -->98 -->98 -->98 -->98 -->99 -->100 -->
Save as the animation (Part 1)
plot_time_series = function(infected, m){
num_cum = unlist(lapply(1:m,
function(x) length(infected[[x]]) ))
p_cum = num_cum/node_number
p = diff(c(0, p_cum))
time = 1:m
plot(p_cum~time, type = "b",
ylab = "CDF", xlab = "Time",
xlim = c(0,total_time), ylim =c(0,1))
plot(p~time, type = "h", frame.plot = FALSE,
ylab = "PDF", xlab = "Time",
xlim = c(0,total_time), ylim =c(0,1))
}
Save as the animation (Part 1)
plot_time_series(infected, 16)
Save as the animation (Part 2)
plot_gif = function(infected){
m = 1
while(m <= length(infected)){
layout(matrix(c(1, 2, 1, 3), 2,2, byrow = TRUE), widths=c(3,1), heights=c(1, 1))
V(g)$color = "white"
V(g)$color[V(g)%in%infected[[m]]] = "red"
plot(g, layout =layout.old, edge.arrow.size=0.2)
title(paste(graph_name, "\n Transmission Rate =", transmission_rate, ", Day", m))
plot_time_series(infected, m)
m = m + 1}
}
Save as the animation (Part 3)
library(animation)
saveGIF({
ani.options(interval = 0.5, convert = shQuote("C:/Program Files/ImageMagick-6.8.8-Q16/convert.exe"))
# start the plot
plot_gif(infected)
}, ani.width = 800, ani.height = 500)
See the animation
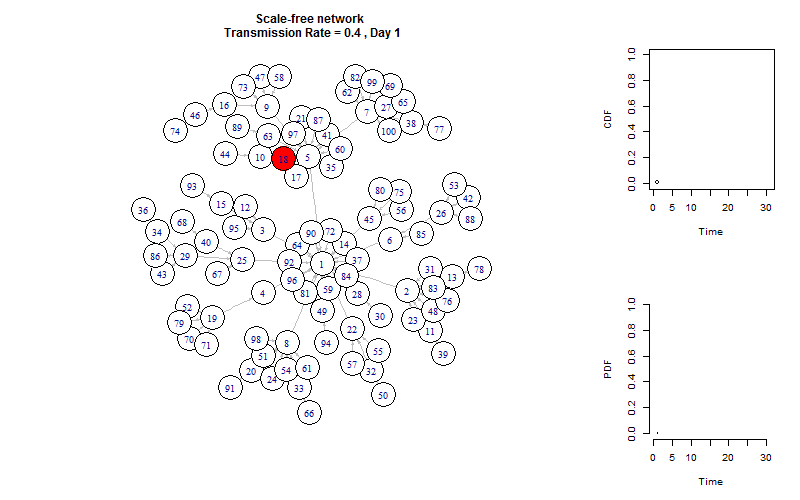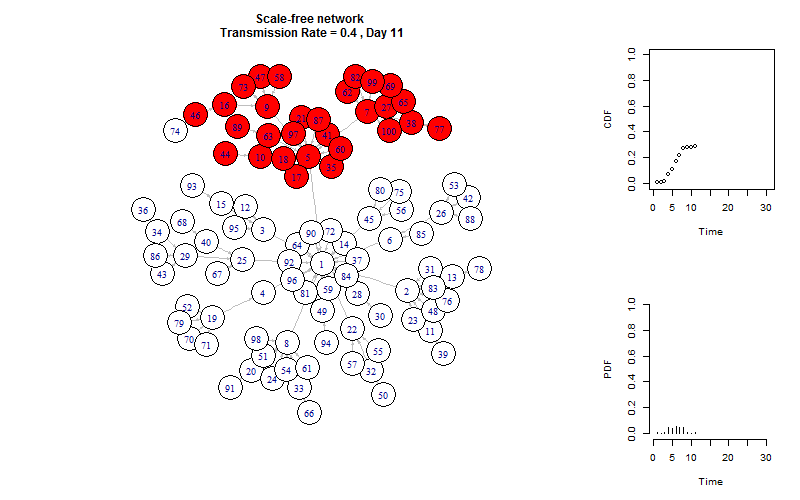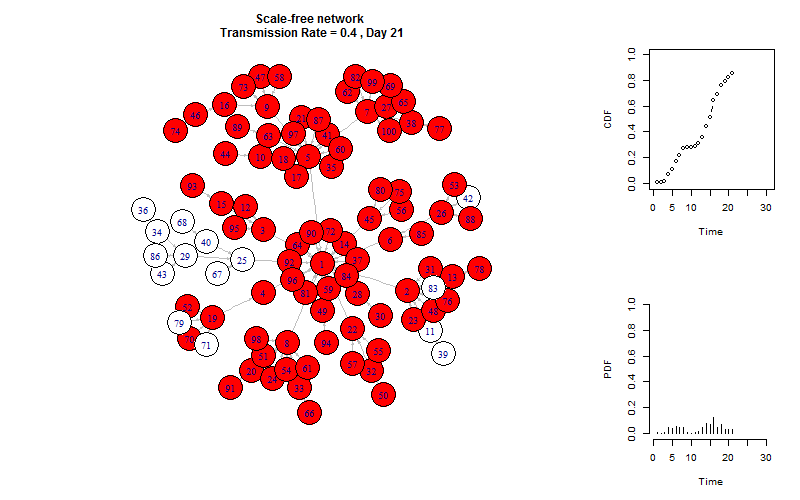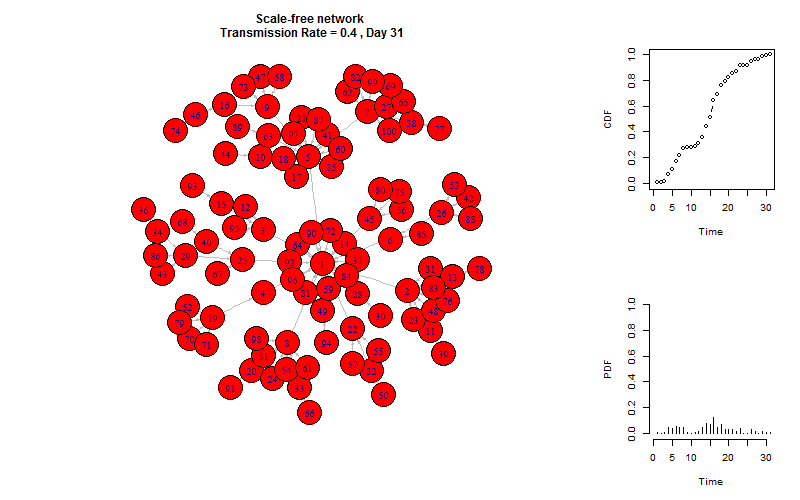
This is the end!
Cheng-Jun Wang
- Web Mining Lab
- Department of Media and Communication
- City University of Hong Kong

